You are a Python expert and you know some math.

So when people ask u,

“Matt how do I compute a vector perpendicular to these two vectors?”

You can just toss this one liner around:

>>> import numpy as np
>>> np.cross([1,0,0], [0,1,0])
array([0, 0, 1])

But what if one day your best friend decides to ask you

“Matt how do I compute the 5-dimensional normal vector to this 4-dimensional hyperplane embedded in 5 dimensional ambient space?”

What would you do?

Well, unfortunately I’m Matt and my Math major friend asked me to do exactly that.

At this point you must be thinking, “isn’t numpy able to do that?”.

Nope, np.cross raises fucking ValueError when you pass in vectors of dimension not equal to 2 or 3.

The Formula

Here is the formula of 4 dimensional cross product (vectors are 4 dimensional)

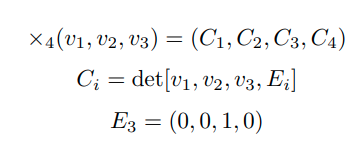
formula for 4 dimensional cross product

That’s basically it, high dimensional ones generalize similarly.

The Code (for arbitrary dimension)

def generalized_cross_product(vectors: np.ndarray) -> List[float]:
    # make sure you pass in a rectangular matrix
    # each row is a x dimensional vector
    
    dim = vectors.shape[1]
    res = []
    for j in range(dim):
        ej = [0] * dim
        ej[j] = 1
        res.append(np.linalg.det(np.vstack([vectors, ej])))
    return res

Mega Confusion ? / Gotchas

  • still, how to compute normal vectors of an hyperplane?

    well, if you want to compute the normal vector of a x-dimensional hyperplane embedded in x+1 dimensional ambient space: first, you gotta find x number of vectors on that plane (or equivalently find x+1 number of not collinear x+1 dimensional points on the plane and subtract them to get vectors). Then pass in each plane vector as a row in the argument to generalized_cross_product

  • Aren’t there many normal vectors, and unit normal vector?

    A hyperplane divides the space to two divisions and it’s only got 2 unique unit normal vectors of the opposite directions. To get the unit normal vector:

      normal_vector = np.array(generalized_cross_product(plane_vectors))
  unit_normal_vector_1 = normal_vector / np.linalg.norm(normal_vector)
  unit_normal_vector_2 = - unit_normal_vector_1

  • The code doesn’t run

    the function definition part of the code used “typing annotation” : np.ndarray and -> List[float]

    do from typing import List on Python >=3.5 before the function

    or delete them on lower Python versions